1. Задание № 181 

Сложность: I
Классификатор алгебры: 1\.1\. Действия с числами, степенями, дробями
Числа и их свойства, сравнение чисел
i
Даны дроби 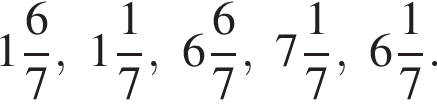 Укажите дробь, которая равна дроби
Укажите дробь, которая равна дроби ![]()
1) 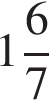
2) 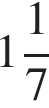
3) 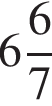
4) 
5) 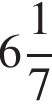
Решение. Выделим в данной дроби целую часть: 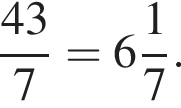
Правильный ответ указан под номером 5.
Ответ: 5
181
5
Сложность: I
Классификатор алгебры: 1\.1\. Действия с числами, степенями, дробями
 равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
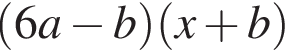
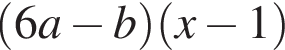

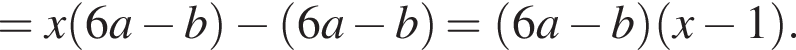

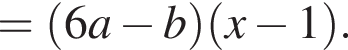
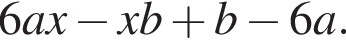
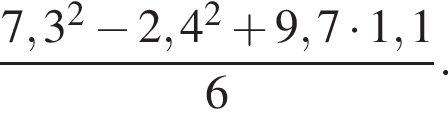
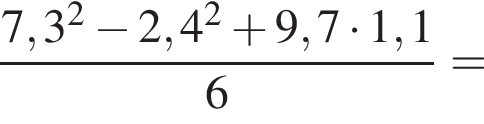
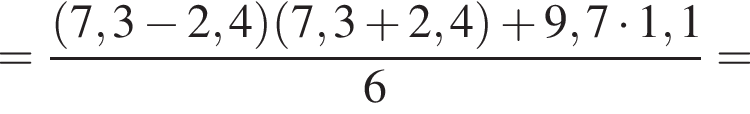
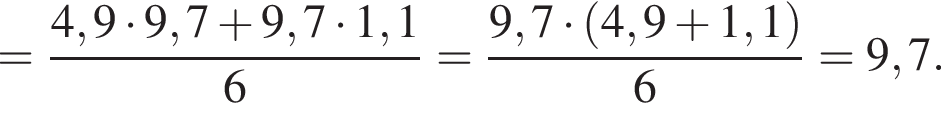
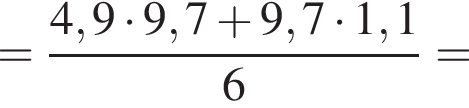
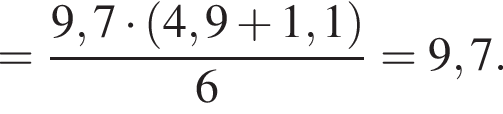
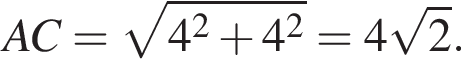

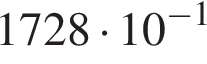
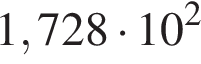
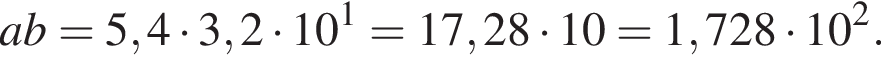
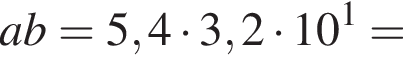

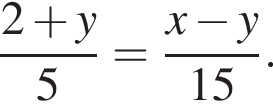
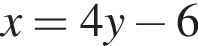
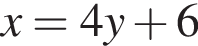


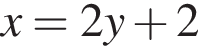
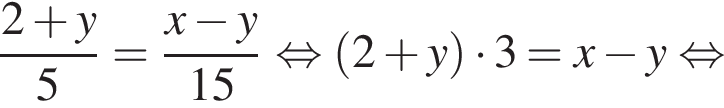
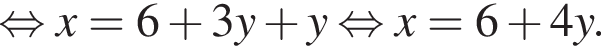
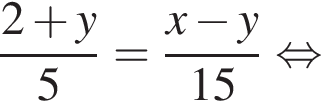
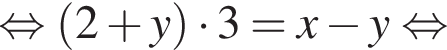


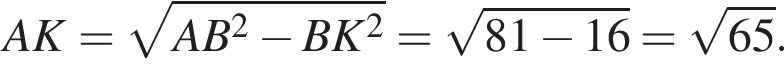

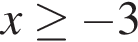

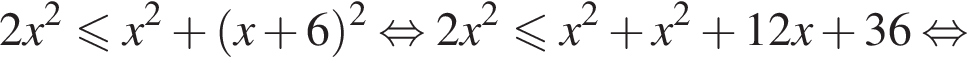

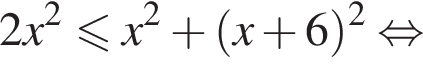
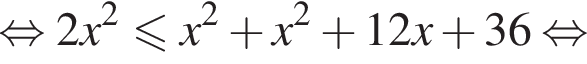
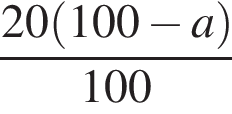
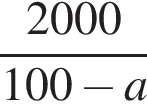
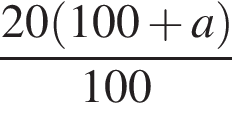
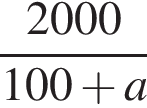
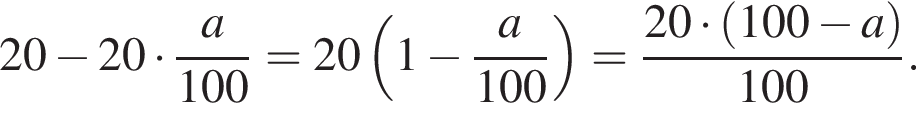
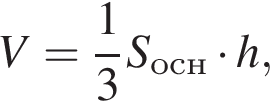 поэтому
поэтому 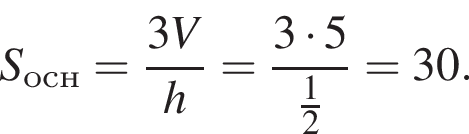
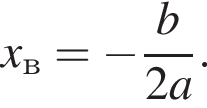 Поэтому
Поэтому 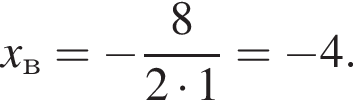 Поскольку y(xв) = −3, имеем:
Поскольку y(xв) = −3, имеем: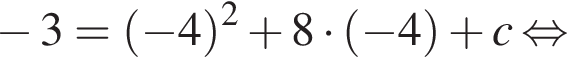

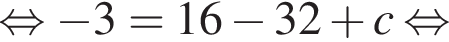
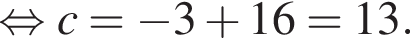
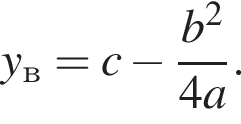
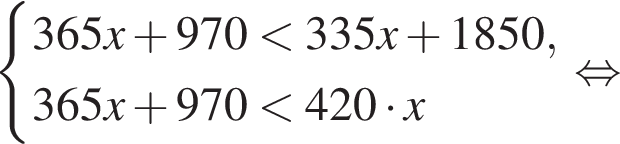
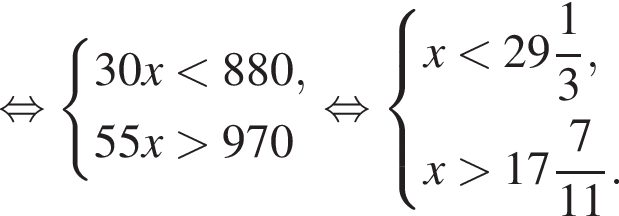
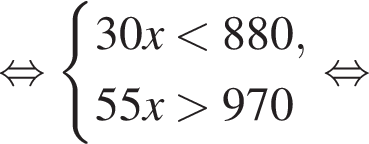
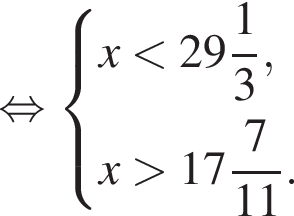
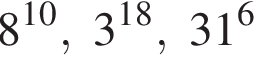 в порядке возрастания.
в порядке возрастания.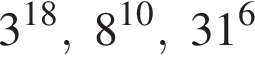
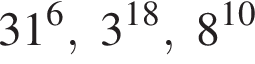
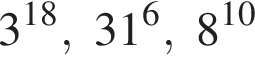
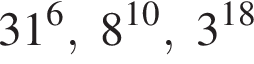
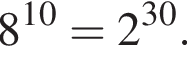 Поскольку все числа положительны, извлечем из каждого корень шестой степени и получим:
Поскольку все числа положительны, извлечем из каждого корень шестой степени и получим: 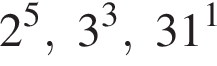 то есть числа 32, 27, 31. Так как 27 < 31 < 32, получаем
то есть числа 32, 27, 31. Так как 27 < 31 < 32, получаем 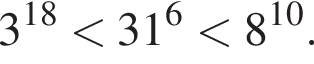
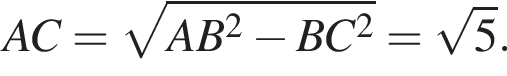 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC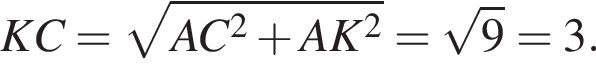
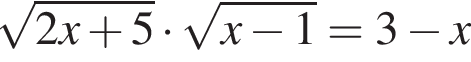 равна (равен):
равна (равен):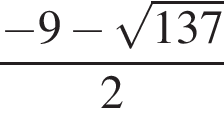
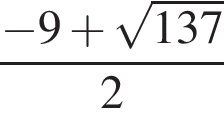
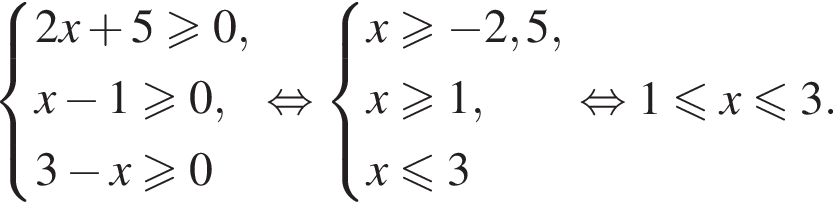
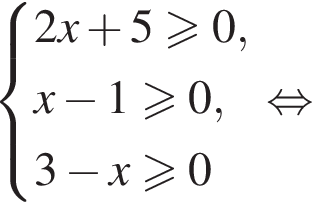
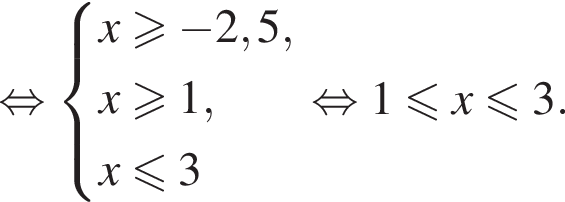
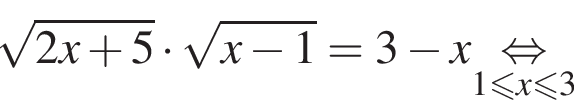
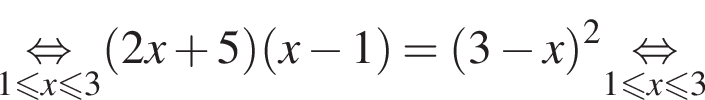
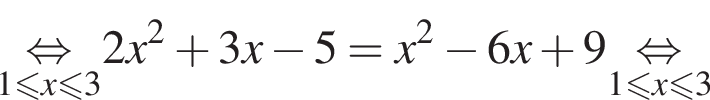
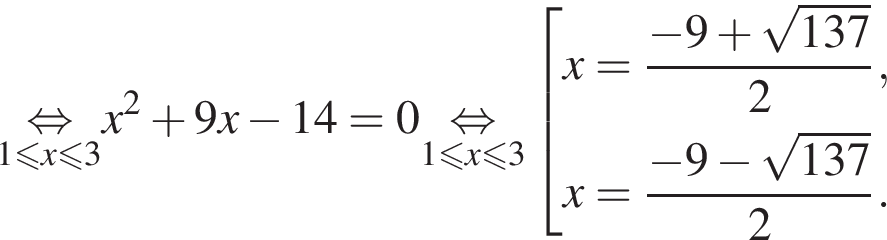
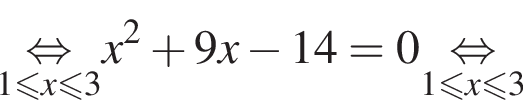
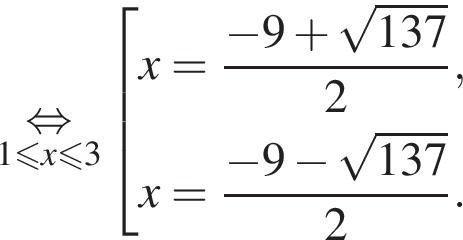
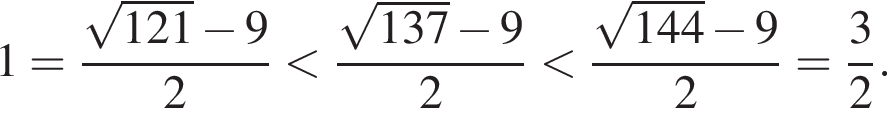
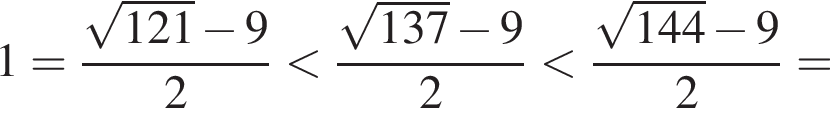
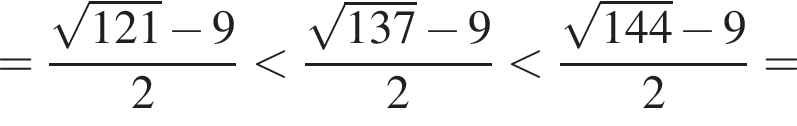
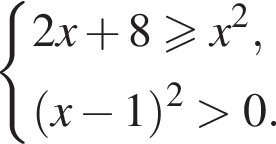
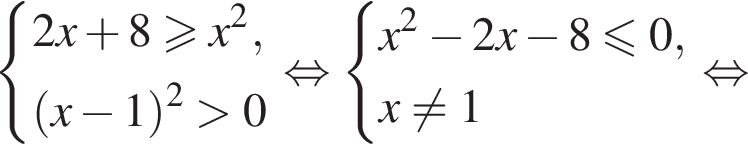
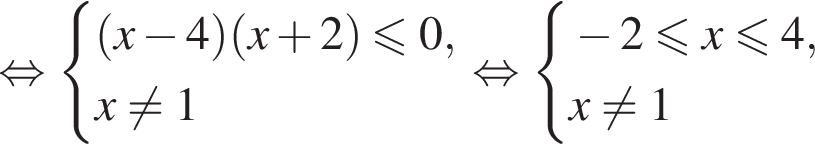
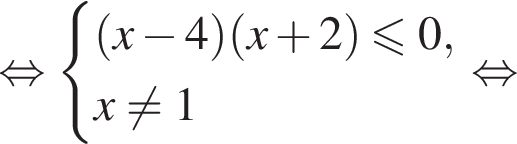
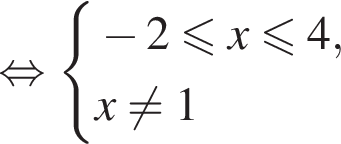
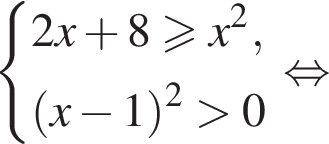
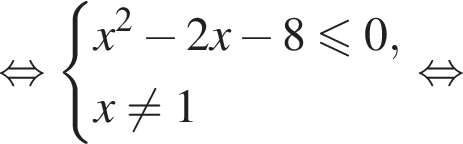
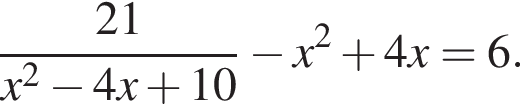
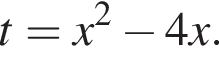 Тогда:
Тогда: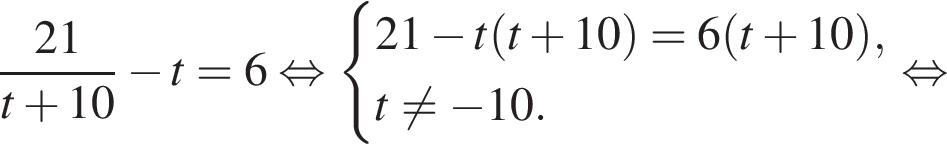
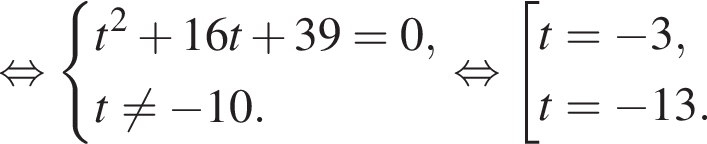
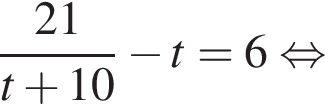
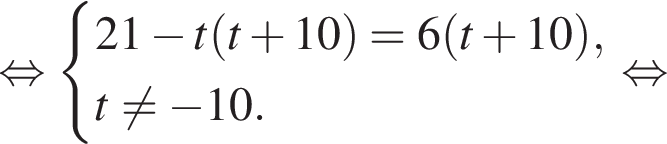
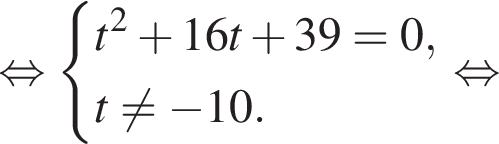
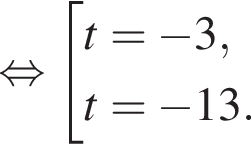
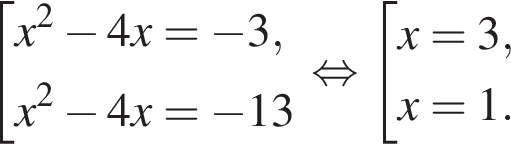
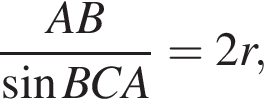 откуда
откуда 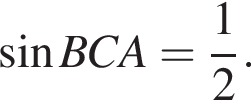 Из прямоугольного треугольника BHC имеем:
Из прямоугольного треугольника BHC имеем: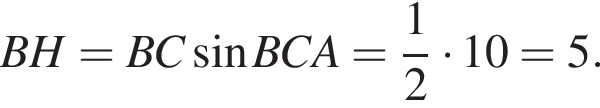
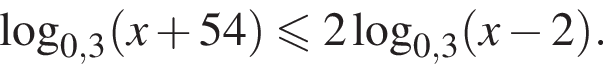
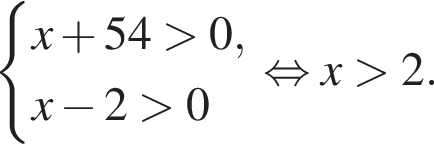
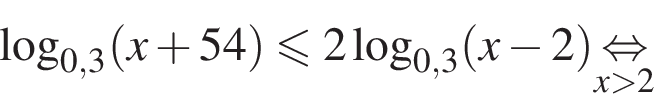
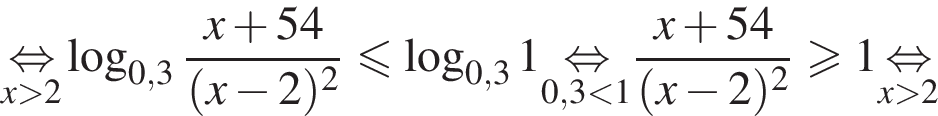
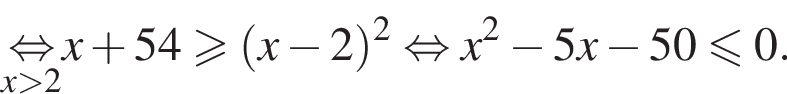
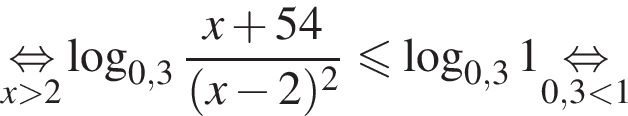
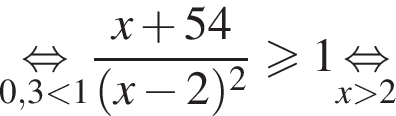

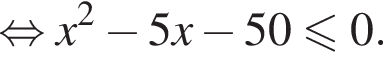
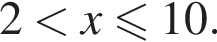 Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.
Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.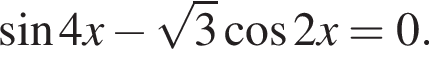
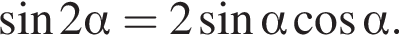 Тогда:
Тогда:
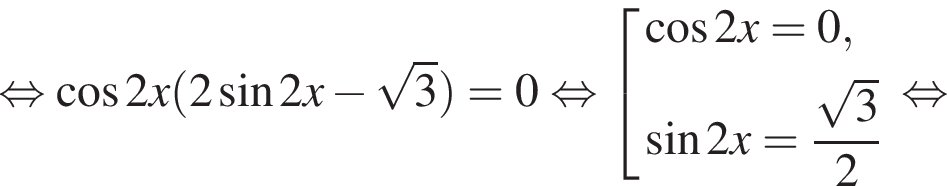
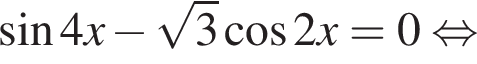

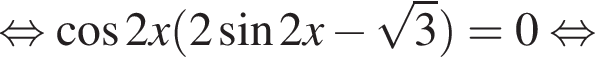
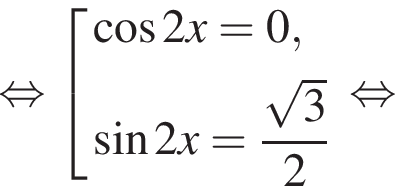
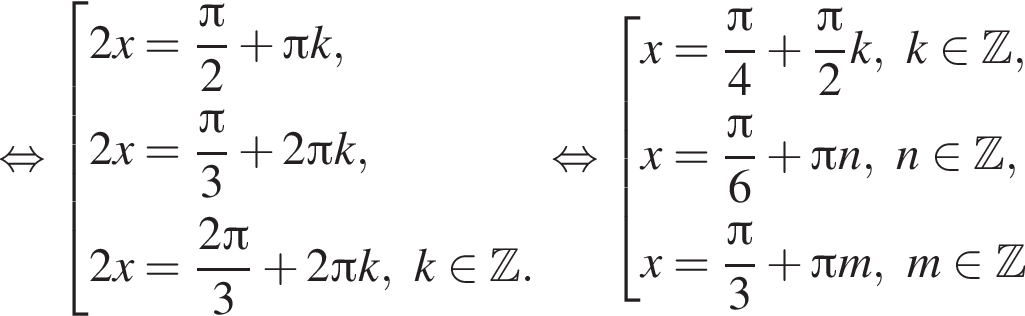
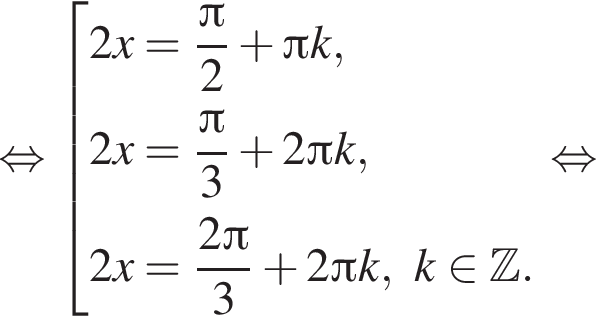
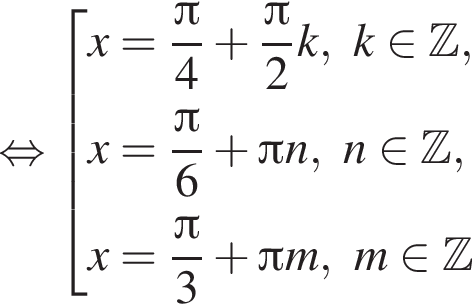
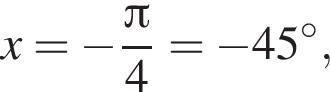 наименьшим положительным решением уравнения является корень
наименьшим положительным решением уравнения является корень 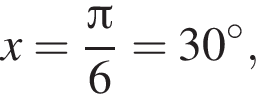 их сумма равна −15°.
их сумма равна −15°.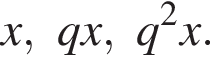
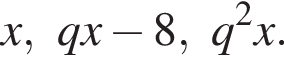
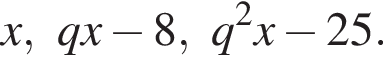
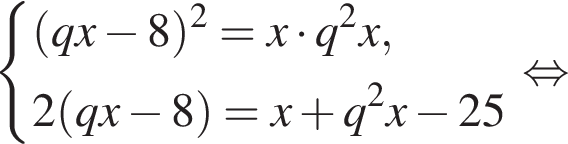
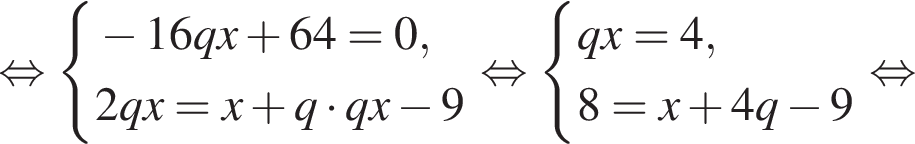
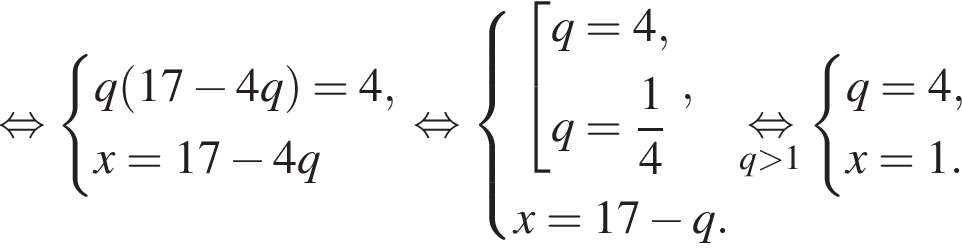
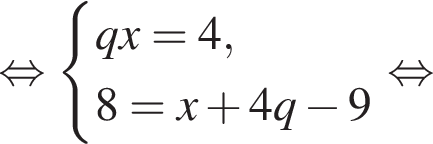
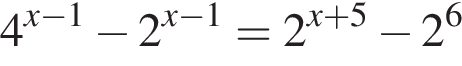 на их количество.
на их количество.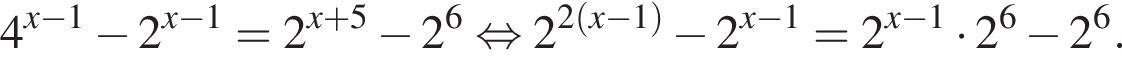
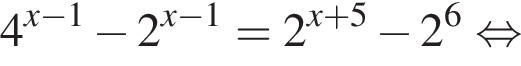
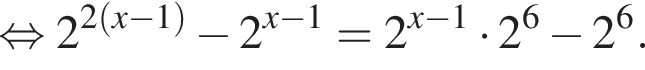
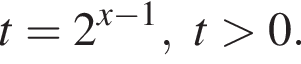 Поэтому:
Поэтому: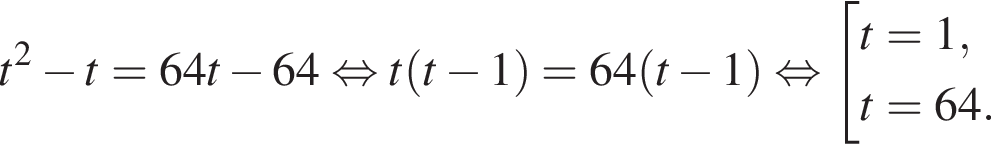

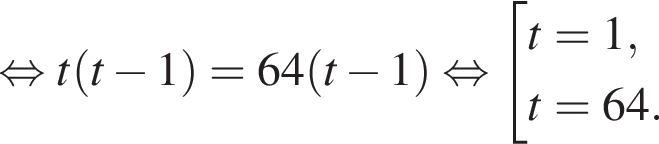

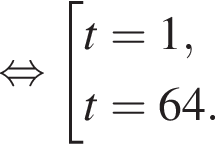
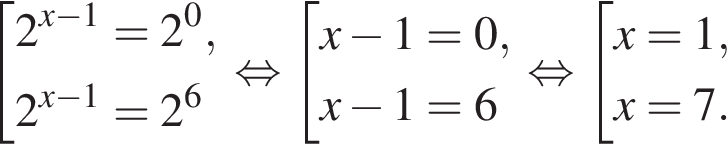
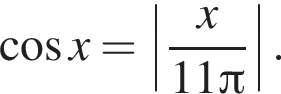

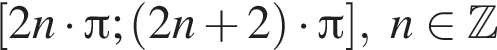 вплоть до
вплоть до 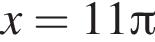 решений нет. На отрезке
решений нет. На отрезке 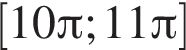 уравнение имеет лишь единственное решение, поскольку при
уравнение имеет лишь единственное решение, поскольку при 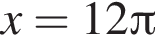 уравнение решений не имеет в силу
уравнение решений не имеет в силу 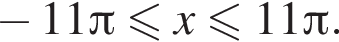 Поэтому на положительной полуоси уравнение имеет 11 решений. В силу четности левой и правой частей уравнения всего имеем 22 решения.
Поэтому на положительной полуоси уравнение имеет 11 решений. В силу четности левой и правой частей уравнения всего имеем 22 решения.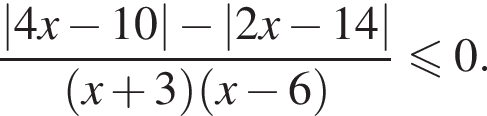
 совпадает со знаком разности
совпадает со знаком разности  имеем:
имеем: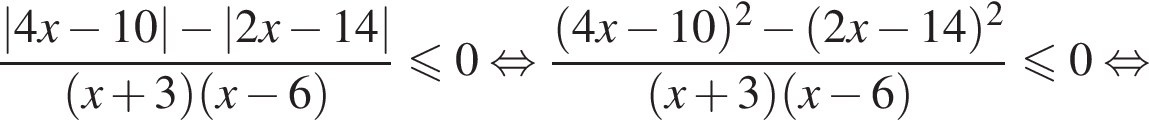
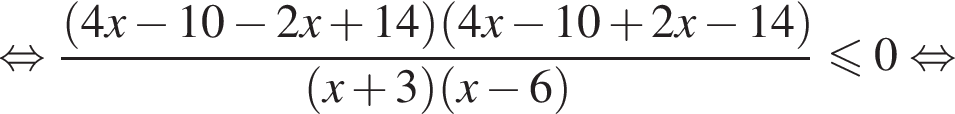
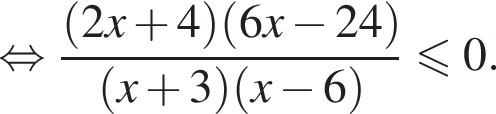
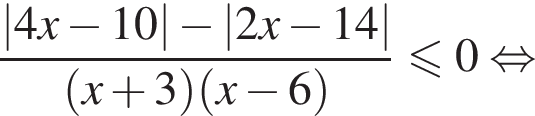
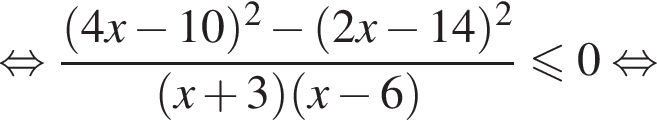
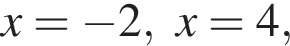 корни знаменателя
корни знаменателя 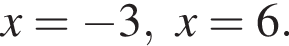 Поэтому:
Поэтому: 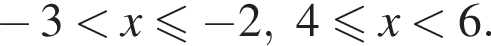 Целые решения — числа −2, 4, 5. Их сумма равна 7.
Целые решения — числа −2, 4, 5. Их сумма равна 7.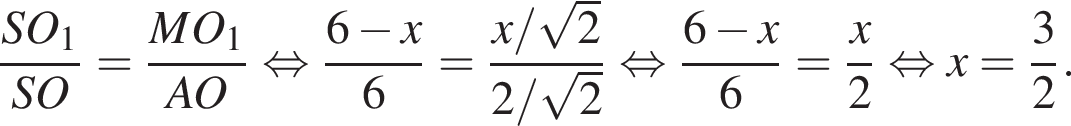
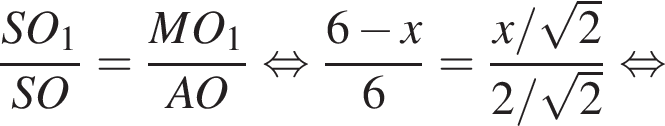
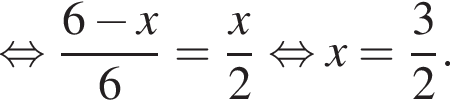
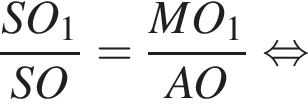
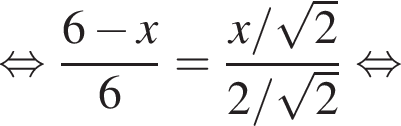
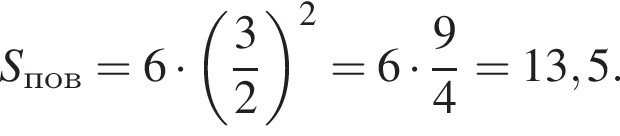
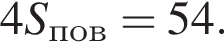
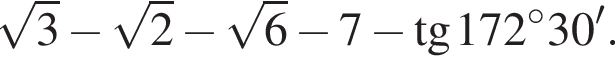
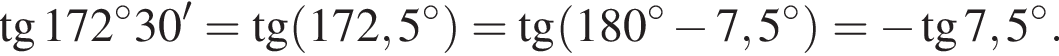
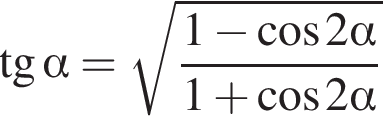 :
: 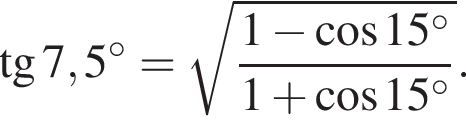



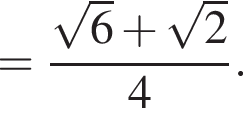
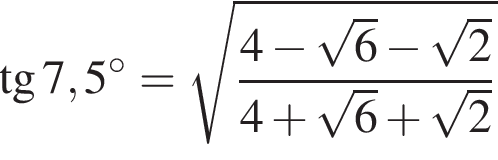
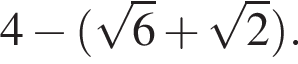 Тогда:
Тогда: 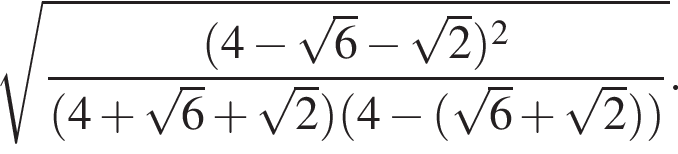
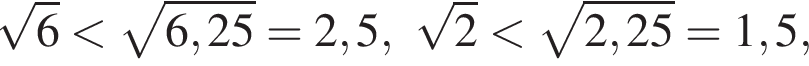
 тогда
тогда 
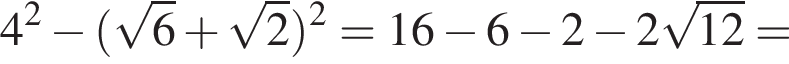

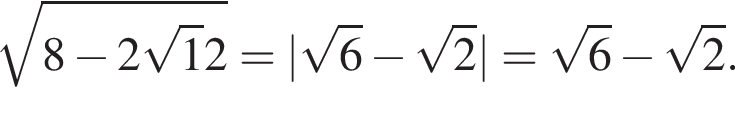 Тогда:
Тогда: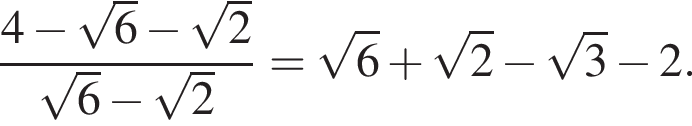
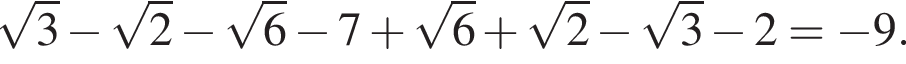
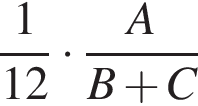 работы.
работы. 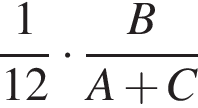 работы.
работы. 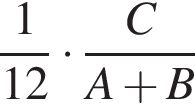 работы.
работы. 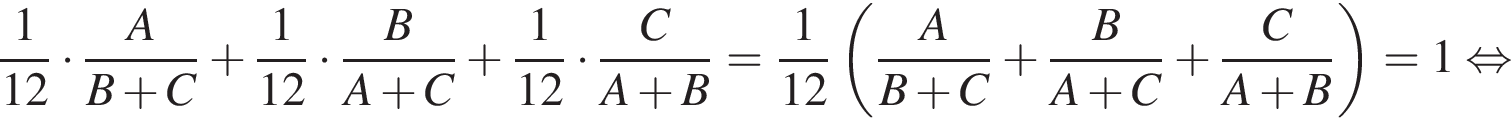
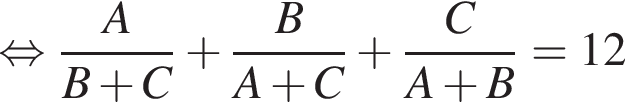
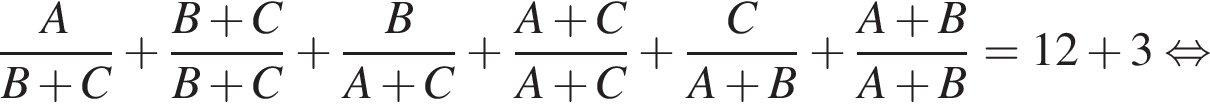
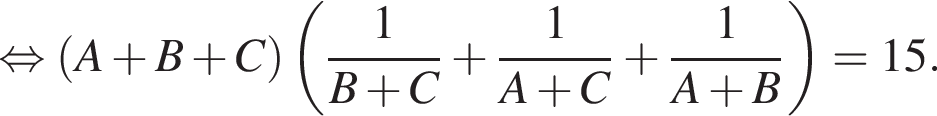
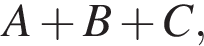 то они выполнили бы работу за:
то они выполнили бы работу за: 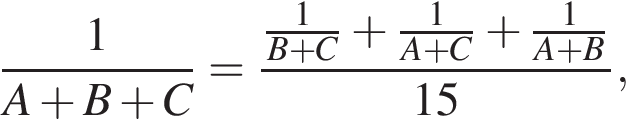
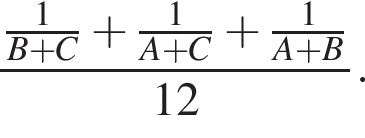 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 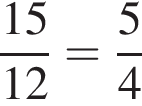 раза быстрее. В ответе будет число
раза быстрее. В ответе будет число